容斥原理

简介

假设班里有10个学生喜欢数学，15个学生喜欢语文，21个学生喜欢编程，班里至少喜欢一门学科的有多少个学生呢？

是 $10+15+21=46$个吗？不是的，因为有些学生可能同时喜欢数学和语文，或者语文和编程，甚至还有可能三者都喜欢。

为了叙述方便，我们把喜欢语文、数学、编程的学生集合分别用$A,B,C$表示，则学生总数等于 $|A\cup B\cup C|$ 。

刚才已经讲过，如果把这三个集合的元素个数 $|A|,|B|,|C|$ 直接加起来，会有一些元素重复统计了，因此需要扣掉 $|A\cap B|,|B\cap C|,|C\cap A|$ ，但这样一来，又有一小部分多扣了，需要加回来，即 $|A\cap B\cap C|$。

即：$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|$

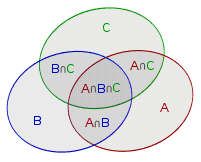
把上述问题推广到一般情况，就是我们熟知的容斥原理。

容斥原理

设 U 中元素有 n 种不同的属性，而第 i 种属性称为 $P_i$，拥有属性 $P_i$ 的元素构成集合 $S_i$，那么

即

证明

对于每个元素使用二项式定理计算其出现的次数。对于 $x$ ，假设它出现在 $T_1,T_2,\cdots,T_m$ 的集合中，那么它的出现次数为

于是每个元素出现的次数为 1，那么合并起来就是并集。证毕。

补集

对于全集 U 下的 集合的并 可以使用容斥原理计算，而集合的交则用全集减去 补集的并集 求得：

右边使用容斥即可。

不定方程非负整数解计数

给出不定方程 $\sum_{i=1}^nx_i=m$ 和 $n$ 个限制条件 $x_i\leq b_i$ ，其中 $m,b_i\leq \mathbb{N}$. 求方程的非负整数解的个数

没有限制时

如果没有 $x_i<b_i$ 的限制，那么不定方程 $\sum_{i=1}^nx_i=m$ 的非负整数解的数目为 $C_{m+n-1}^{n-1}$.

略证：插板法。

相当于你有 m 个球要分给 n 个盒子，允许某个盒子是空的。这个问题不能直接用组合数解决。

于是我们再加入 n-1 个球，于是问题就变成了在一个长度为 m+n-1 的球序列中选择 n-1 个球，然后这个 n-1 个球把这个序列隔成了 n 份，恰好可以一一对应放到 n 个盒子中。那么在 m+n-1 个球中选择 n-1 个球的方案数就是 $C_{m+n-1}^{n-1}$ 。

容斥模型

接着我们尝试抽象出容斥原理的模型

1. 全集 U：不定方程$\sum_{i=1}^nx_i=m$的非负整数解

2. 元素：变量$x_i$.

3. 属性：$x_i$的属性即 $x_i$ 满足的条件，即$x_i\leq b_i$的条件

目标：所有变量满足对应属性时集合的大小，即$|\bigcap_{i=1}^nS_i|$.

这个东西可以用 $\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right|$ 求解。$|U|$ 可以用组合数计算，后半部分自然使用容斥原理展开。

那么问题变成，对于一些$\overline{S_{a_i}}$的交集求大小。考虑 $\overline{S_{a_i}}$ 的含义，表示 $x_{a_i}\geq b_{a_i}+1$ 的解的数目。而交集表示同时满足这些条件。因此这个交集对应的不定方程中，有些变量有 下界限制 ，而有些则没有限制。

能否消除这些下界限制呢？既然要求的是非负整数解，而有些变量的下界又大于 0，那么我们直接 把这个下界减掉 ，就可以使得这些变量的下界变成 0，即没有下界啦。

因此对于$\biggl| \bigcap_{j=1}^{k} S_{a_j} \biggr|$的不定方程形式为$\sum_{i=1}^nx_i=m-\sum_{i=1}^k(b_{a_i}+1)$

于是这个也可以组合数计算啦。这个长度为 k 的 a 数组相当于在枚举子集。

HAOI2008 硬币购物

4 种面值的硬币，第 i 种的面值是 $C_i$ 。n 次询问，每次询问给出每种硬币的数量$D_i$和一个价格$S$ ，问付款方式。

$n\leq 10^3,S\leq 10^5$

如果用背包做的话复杂度是$O(4nS)$，无法承受。这道题最明显的特点就是硬币一共只有四种。抽象模型，其实就是让我们求方程$\sum_{i=1}^4C_ix_i=S,x_i\leq D_i$的非负整数解的个数。

采用同样的容斥方式，$x_i$的属性为 $x_i\leq D_i$ . 套用容斥原理的公式，最后我们要求解

也就是无限背包问题。这个问题可以预处理，算上询问，总复杂度$O(4S+2^4n)$ .

#include <bits/stdc++.h>

using namespace std;
const int S = 1e5 + 5;
int c[5], d[5], n, s;
long long f[S];

int main() {

    cin >> c[1] >> c[2] >> c[3] >> c[4] >> n;
    f[0] = 1;
    for (int j = 1; j <= 4; j++)
        for (int i = 1; i < S; i++)
            if (i >= c[j]) f[i] += f[i - c[j]];
    for (int i = 1; i <= n; i++) {
        cin >> d[1] >> d[2] >> d[3] >> d[4] >> s;
        long long ans = 0;
        for (int j = 1; j < 16; j++) {
            int m = s, bit = 0;
            for (int k = 1; k <= 4; k++)
                if ((j >> (k - 1)) & 1) m -= (d[k] + 1) * c[k], bit++;
            if (m >= 0) ans += (bit % 2 * 2 - 1) * f[m];
        }
        cout << f[s] - ans << endl;
    }
    return 0;
}